Jaime Núñez Miller, socio fundador de Bankabit y de Zentank, veterano de la comunidad Bitcoin y responsable del capítulo 9 del libro (“Criptografía y consenso aplicado a la blockchain”), firma el presente anexo donde incide en otras cuestiones importantes que sirven para ampliar nuestros conocimientos sobre las claves y los secretos de la criptografía y su aplicación en la tecnología blockchain.
***
ECDSA (Elliptic Curve Digital Secure Algorithm)
La criptografía de curva elíptica es ya una de las más populares, es extremadamente segura desde el punto de vista matemático y comparado con RSA, ECDSA utiliza claves más pequeñas y en general es una implementación más eficiente. ECDSA es por el momento el esquema utilizado por Bitcoin, Ethereum y la mayor parte de los protocolos blockchain.
La magia de ECDSA es la que nos permitirá obtener una clave pública a partir de una clave privada. Con ambas claves ya podremos firmar transacciones y verificar luego las firmas tal y como se explica en el apartado de «Criptografia asimétrica» (pag. 209) y «Firma de una transacción de Bitcoin» (pág. 239) en el libro.
Aquí exploraremos el funcionamiento de ECDSA en su especificación secp256k1 (la usada en protocolos blockchain) para obtener la clave publica K a partir de una clave privada aleatoria k y de un punto dado G llamado punto base que siempre es el mismo. Este punto es público, se determina por el protocolo y no cambia nunca.
k * G = K Clave privada * Punto base = Clave pública
Las curvas elípticas tienen ciertas características que las hacen especiales en el mundo de la criptografía. A diferencia de RSA que multiplica dos grandes números primos para obtener la clave pública, ECDSA utiliza una serie de operaciones aritméticas especiales sobre puntos en una curva elíptica. Para ello se recurre a dos tipos de operaciones especiales: la suma y la multiplicación de puntos en la curva. En primer lugar veremos en qué consiste la suma y la multiplicación y luego explicaremos cómo se calcula la clave pública.
Son conceptos algo complejos, pero los hemos simplificado todo lo posible. La explicación está orientada a un público general, así que si tienes algo de paciencia te ayudarán a entender cómo ECDSA es capaz de generar una clave pública de forma segura.
Cómo se suman puntos en la curva elíptica
Partiendo de dos puntos (los llamaremos P y Q) trazamos una recta que se cruzará (no siempre) con la curva en un punto al que llamaremos -R. Para obtener luego la suma de P+Q bastará con reflejar el punto -R sobre el eje X y así llegar el punto R que será la suma geométrica de P+Q.
P + Q = R
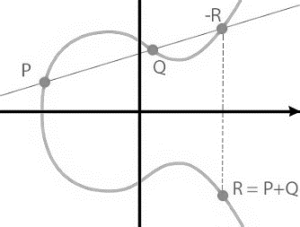
En el caso de que la recta no cortara la curva en ningún otro punto y se perdiera en el infinito diremos que corta la curva en el infinito o punto del infinito O. En este caso la suma sería
P + Q = O
Recordemos que trabajamos con coordenadas. Veamos un ejemplo concreto usando geometría y sin recurrir a fórmulas aritméticas. Si nos dan dos puntos cualesquiera en la curva, P y Q, por ejemplo (-2.0, 1.4) y (0.2, 1.7) nos bastaría una regla y un lápiz para trazar una recta y obtener el punto -R. Luego reflejamos -R sobre el eje X y obtenemos las coordenadas de R tal y como vemos en la siguiente ilustración:
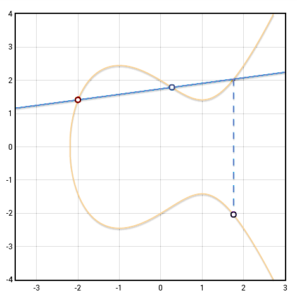
El resultado R en este caso sería (1.7, -2.0)
Sin embargo ¿qué pasaría en el caso de que P y Q fueran el mismo punto?. En ese supuesto no podríamos trazar una recta para obtener R por lo que recurrimos a la tangente del punto P para obtener la recta que necesitamos.
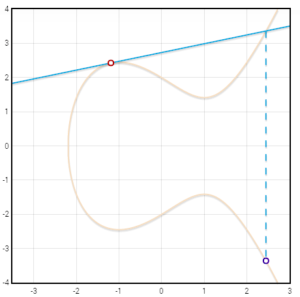
Por ejemplo si tenemos el punto P (-1.1, 2.4) que en este caso es el mismo que el punto Q, solo tendríamos que trazar la tangente de P para obtener -R y luego llegar a R. Miramos el gráfico y deducimos que R es el punto (2.4, -3.3).
La fórmula aritmética de este tipo de suma (para obtener R a partir de P y Q) es la siguiente:
Dados (x1, y1), (x2, y2) debemos hallar (x3,y3) = (x1, y1), (x2, y2)
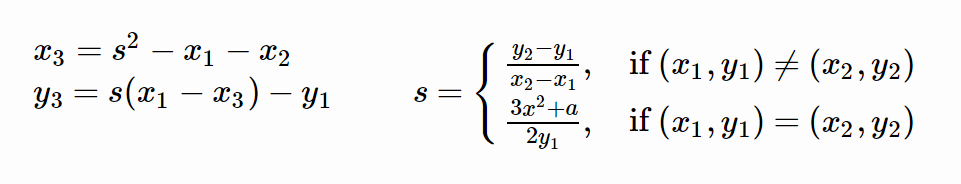
Cómo se multiplican puntos en la curva elíptica.
Ya hemos visto el cálculo de R con la suma de P y Q cuando P y Q son distintos:
P + Q = R
y también cuando ambos P y Q son mismo punto:
P + P = 2P = R
Por tanto, el cálculo si utilizáramos más de dos puntos iguales para obtener R, sería:
P + P + P + P + P + ... + P = nP
Veamos un ejemplo con n = 5. Una forma de hacerlo sería esta:
2 * P = 2P 2P + P = 3P 3P + P = 4P 4P + P = 5P
Si usamos 2 como multiplicador podríamos hacerlo en solo tres pasos:
2 * P = 2P 2 * 2P = 4P 4P + P = 5P
A esta forma de “acelerar” la multiplicación le llamaremos “doblar y sumar” o multiplicación escalar y nos permite llegar al resultado final 5P más rápidamente. Si el número n fuera mucho mayor podríamos incrementar el multiplicador y el cálculo se realizaría exponencialmente más rápido. Bitcoin utiliza números de 1077 cifras o 256 bits que pueden requerir cerca de 250 pasos. Este sistema se utiliza en varios algoritmos de clave pública, no solo ECDSA.
Campos finitos
Las fórmulas aritméticas nos suelen dar resultados con decimales y eso ocasiona un problema que hay que resolver. Algunos decimales son irracionales y no terminan nunca, por ejemplo 3,14159265358… etc. y nuestros ordenadores no disponen de espacio infinito para almacenar este tipo de números. Por supuesto que nuestras computadoras pueden hacer aproximaciones, sin embargo, si les preguntáramos si es cierto que 1,9999 = 2 no sabrían qué responder. Para solucionar este problema deberemos usar sólo los puntos de la curva que se puedan representar con números enteros, sin decimales. Todos los demás los obviamos.
De esta forma establecemos qué tipo de elementos forman parte de nuestro campo de trabajo. Si nuestro campo fuera una mesa de billar, sería el equivalente a definir qué características deben de tener las bolas con las que queremos jugar. En este ejemplo, nuestras bolas de billar se llaman números enteros. En nuestro campo sólo habrá números enteros y eso lo van a agradecer mucho nuestros ordenadores.
Os podéis imaginar que a nuestro ordenador tampoco le gusta jugar en mesas de billar infinitas así que tendremos que definir unos límites. Con esto logramos que las bolas que se vayan a salir reboten y siempre queden dentro de la mesa. Para ello nos valdremos de un concepto matemático llamado aritmética modular. Si eres capaz de leer las horas de un reloj digital ya sabes lo que es aritmética modular. Veamos un ejemplo para entender en qué consiste. Si ahora fueran las 11 de la noche (23:00 h) y te tuvieras que despertar en 8 horas, pondrías la alarma de tu despertador a las 07:00 h y no a las 31:00 h. Cuando la hora llega a las 24:00 se empieza a contar de nuevo a partir de las 00:00. Ese reloj estaría contando en módulo 24 o (mod 24). Por tanto el 24 es el número máximo en ese campo.
El cálculo en nuestro despertador es el siguiente
23h + 8h = 31h 31 ≡ 7 mod 24
lo que se lee de la siguiente forma: “31 es congruente con 7, cuando estamos en módulo 24”
En el caso del estándar de curva elíptica secp256k1 utilizado por Bitcoin el cuerpo finito son todos los números enteros en donde el límite de elementos es un número primo enorme, concretamente:
p=115792089210356248762697446949407573530086143415290314195533631308867097853951
La razón de elegir este número es que es primo, su longitud es de 256 bits y su expresión binaria tiene 127 ceros y 129 unos, lo que facilita los cómputos.
Anteriormente vimos que a curva elíptica usada por Bitcoin era del tipo y2 = x3 + 7. Ahora ya podemos avanzar un poco más y definir la curva elíptica en un campo finito (F) de números enteros, módulo p. En donde p es el número primo de enormes dimensiones que hemos visto arriba.
y2 = x3 + 7 sobre (Fp)
Las curvas elípticas definidas sobre cuerpos finitos en donde el límite p es un número primo grande, como es nuestro caso, son de gran interés criptográfico debido a la enorme dificultad que arroja el problema del logaritmo discreto cuando se plantea sobre este tipo de cuerpos.
Las multiplicaciones escalares necesarias para obtener el punto que representa la clave pública siguen siendo fáciles y rápidas, mientras que el logaritmo discreto se convierte en un problema de muy difícil resolución, que es precisamente la propiedad que se busca para una función de clave pública unidireccional.
Al representar nuestras curvas elípticas en cuerpos finitos, el gráfico de la curva no queda tan elegante. Recordemos que en el cuerpo finito Fp ya no contamos con decimales, por lo que el gráfico parece un grupo de puntos inconexos más que una curva. Sin embargo esos puntos conservan las mismas propiedades aritméticas que la curva.
Si queremos enumerar los puntos de la curva debemos proponer primero un punto inicial. A ese punto le llamamos “punto base” que representamos aquí con la letra G. Los puntos de la curva se irán añadiendo a la gráfica a medida que multiplicamos G por cada número entero hasta llegar al límite máximo de nuestro campo finito. Por ejemplo, los puntos en una curva elíptica módulo 29 (cuyo límite es 29) se muestran en la siguiente ilustración que contiene cada uno de sus 29 puntos.
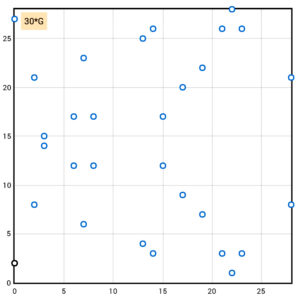
1*G = (0,2) 2*G = (6,17) 3*G = (22,1) . . . 28*G = (22,28) 29*G = (6,12) 30*G = (0,27)
En éste gráfico podemos ver todos los puntos de la curva porque el módulo es muy pequeño, pero sería imposible visualizarlos al completo si usáramos límites mucho mayores.
Calcular la clave pública
La clave privada k será un número entero elegido al azar entre los que forman parte del grupo o cuerpo finito que hemos definido, en nuestro caso un número entre 1 y p-1 en donde p es el número primo visto anteriormente. La clave pública es el punto K que se obtiene al multiplicar la clave privada k por el punto base G.
k * G = K Clave privada * Punto base = Clave pública
Recordemos que el punto base G (también llamado generator point) es siempre el mismo punto para todas las claves y viene dado por la especificación secp256k1 usada en el protocolo Bitcoin. Así pues se trata de multiplicar un punto en la curva elíptica, o sumar k veces el punto base G en la curva aplicando el procedimiento de suma de puntos visto antes.
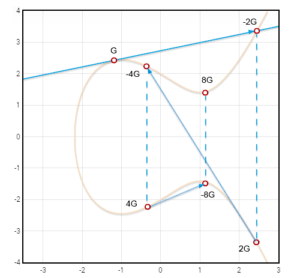
El punto base sería el punto P en esa primera curva, la que usaba números reales en vez de números enteros que es la que usaremos para visualizarlo mejor. El proceso sería el siguiente:
- Trazamos la tangente de G (que es el punto P).
- El punto donde corta la curva es en punto -2G que reflejamos sobre el eje X para llegar al punto 2G.
- Trazamos la tangente de 2G.
- El punto donde corta la curva es en punto -4G que reflejamos sobre el eje X para llegar al punto 4G.
- Trazamos la tangente de 4G.
- El punto donde corta la curva es en punto -8G que reflejamos sobre el eje X para llegar al punto 8G.
Repetiremos el mismo proceso hasta llegar a kG y obtener las coordenadas de K (kG = K) que será nuestra clave pública.
Para entenderlo mejor lo visualizamos en una curva de números reales en vez de enteros:
Terminamos este artículo resaltando los siguientes puntos:
- La clave privada no es más que un número aleatorio sobre el que podemos realizar cálculos matemáticos normales.
- La clave pública en cambio es un punto en una curva elíptica sobre el que sólo se pueden realizar operaciones de suma y multiplicación, pero no se pueden dividir.
- Es fácil calcular la clave pública usando el sistema de multiplicación escalar y prácticamente imposible de obtener la clave privada mediante fuerza bruta.
- Es muy importante que la clave privada sea aleatoria. La mayor parte de los problemas de seguridad detectados hasta el momento se deben a una mala implementación a la hora de generar la clave privada.


